
Therefore, any new observation randomly withdrawn from the same population is not necessarily compatible with the former point estimate because bias was not necessarily the same. According to theory, any point estimate is bound to its sample by an instant bias that depends on the randomness that occurred at the time of the sampling process ( 6). In both of these applications, a sample is drawn once from the population to find out the estimate of the true parameter, afterwards the value is repeatedly applied to a number of new individuals or items to identify them.
In this scenario, a pair of extreme percentiles, often 0.5 th - 99.95 th or 2.5 th - 97.5 th that cut-off 1% or 5% population, respectively, are used to find those subjects whose testing seems to exceed the expected homeostatic variability in a biological parameter ( 5). Another quality application concerns establishing reference intervals for interpreting laboratory tests results ( 4). the 25 th, 50 th and 75 th percentiles collectively known as “quartiles”) are commonly employed to attribute a progressively higher level of performance ( 3). A set of central percentiles that partition the population into equally sized ranges of values ( e.g. Percentiles are also useful tools in the field of quality management to show the distribution of observed performance data and for attributing quality grading and goals in extra-analytical processes through indicators ( 2). Owing to this, they are broadly applied in biomedical field where non-normality due to outlier contamination or natural skewness is commonly observed. Percentiles and quantiles are statistics used for summarizing the relative location of data within a set according to their magnitude and independently from a particular underlying probability distribution ( 1). We also show that both nonparametric and bootstrap methods suit well the CI of central percentiles that are used to derive performance specifications through quality indicators of laboratory processes whose underlying distribution is unknown. The result of our numerical simulations is that parametric methods are always more accurate regardless of sample size when the procedure is appropriate for the distribution of results for both extreme (2.5 th and 97.5 th) and central (25 th, 50 th and 75 th) percentiles and corresponding quantiles. In this work we discuss three methods to estimate CI on quantiles and percentiles using parametric, nonparametric and resampling (bootstrap) approaches.
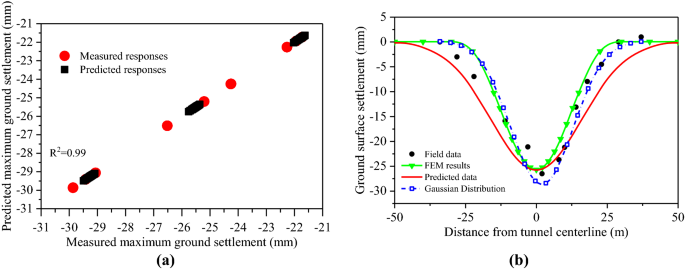
They are commonly intended as the sample estimate of a population parameter and therefore they need to be presented with a confidence interval (CI).
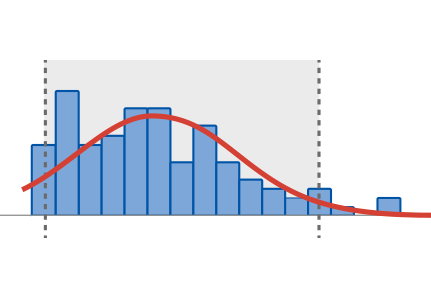
Quantiles and percentiles represent useful statistical tools for describing the distribution of results and deriving reference intervals and performance specification in laboratory medicine.


 0 kommentar(er)
0 kommentar(er)
